Everything About the Degrees of Freedom of a Robot

In this post, you will learn ANYTHING that you’ve ever needed to know about the degrees of freedom of a robot. You will become familiarized with a general formula to find the degrees of freedom of any mechanism, not just robotic arms.
The degrees of freedom of a robot is the dimension of the robot’s C-space, which is the minimum number of real numbers needed to represent the robot’s configuration.
As we saw in the previous post, the robot’s configuration is our answer to the question where is the robot? And we also saw different ways to represent the configuration of the robot.
The minimum number of real numbers that are needed for our representation is called the degrees of freedom.
Degrees of Freedom of a Rigid Body in a 3D Space
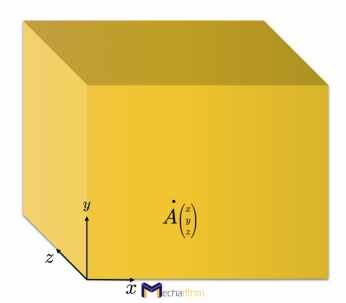
A rigid body in three-dimensional space has six degrees of freedom (DOFs). Three of them are for the position: motion along the x, motion along the y, and motion along the z, and three are for orientation: rotation around x or roll, rotation around y or pitch, and rotation around z or yaw:
You can also imagine this by taking three points on the rigid body. For the first point, there are three freedoms x,y, and z, and no constraints:
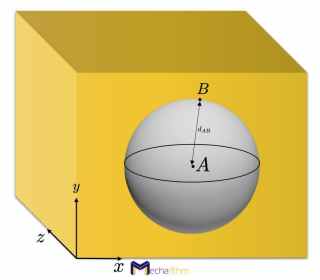
For the next point, we know that the distance between two points on a rigid body should be constant. So, point B can only be on the surface of a sphere with a center at A, which gives us two rotational DOFs. In other words, three coordinates for B minus one independent constraint gives two real freedoms:
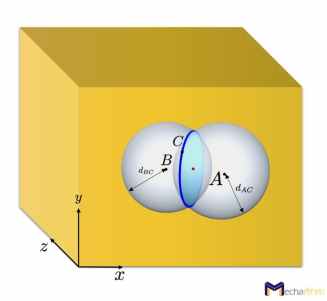
For the third point C, this point’s distance to points A and B should be constant. So, point C can only be on the circle of the intersection of two spheres, giving us one rotational degree of freedom. In other words, with three coordinates for point C and two independent constraints, we will have one DOF:
For point D and so on, the point’s position is fully determined, and there is no more freedom in choosing the place of those points.
Degrees of Freedom of a Rigid Body in a 2D Space
With the same analogy, we can say that the rigid body on a 2D plane has three degrees of freedom. Two linear DOFs and one rotational DOF:
You can also take 3 points on the rigid body and use the same reasoning as before to see that the first point has two linear freedoms and no constraints, the second point will be on a circle centered at the first point, so two coordinates minus one distance constraint is one rotational DOF, and the location of the 3rd point can be fully determined so it will have no degrees of freedom. So overall, a rigid body on a 2D plane has 3 DOFs.
Now think about the DOFs of a rigid body in a 4D space. How many of them are linear, and how many are angular?
Robot Joints Put Constraints on the Motion of the Robot Links Reducing Their Degrees of Freedom (DOFs)
We have seen that a rigid body in a 2D space has Three DOFs, but why does a two-DOF planar robot with two rigid bodies have only two DOfs?

The answer to this question lies in the constraints that its joints put on the links’ movement with respect to each other. This robot has two revolute or hinge joints. Each of the joints put two constraints on the movement of the links. That is, its links can only rotate around the z-axis.
Degrees of Freedom (DOFs) of a 3R Robot Arm
If we imagine a robot in 3D like a 3R robot (with three revolute joints) in space with three revolute joints, the revolute joint (R) will put five constraints on the motion of one link with respect to the other link. So again, it will provide only one DOF:
So, we can conclude that constraints on the robot links come from joints. But how many different joints are used in robots?
Types of Different Joints Used in Robots
Revolute (Rotary) Joints Provide One degree-of-freedom (DOF) for the Robot Links
As we saw in the industrial robot of the previous video, a revolute joint is like a door hinge. It provides one DOF of motion between two bodies that it connects. The rotation is around the joint axis, and the positive rotation can be determined using the right-hand rule:
According to the RHR, if your thumb is in the direction of the joint axis, the positive rotation is the direction your other 4 fingers curl.
Linear (sliding) Joints Provide One degree-of-freedom (DOF) for the Robot Links
A linear, sliding, or prismatic joint (P) provides a linear motion between two links. It will again provide only one DOF between two links:
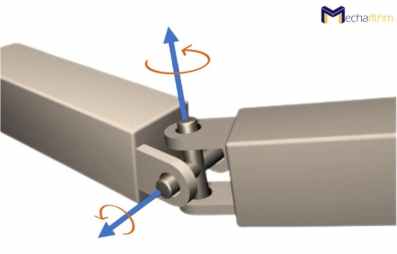
Universal Joints (U) Provide Two Degrees of Freedom for the Links they Connect
Next is the universal (U) joint, which is two revolute joints with joint axes orthogonal to each other thus, it can provide two rotational DOFs around roll and pitch axes that are x and y axes:
Spherical Joints (S) Provide Three Degrees of Freedom Between the Connecting Links
The spherical (S), ball-and-socket, or shoulder joint can provide three DOFs, which are two degrees of freedom of the U joint plus spinning about the joint axis:
Cylindrical Joints (C) Provide Two Degrees of Freedom Between the Connecting Links
Next is a cylindrical (C) joint that can provide an independent translation and rotation about a single fixed joint axis; thus, it has two DOFs. You can watch a short video of the cylindrical joint HERE!
Helical Joints (H) Provide One Degree of Freedom (DOF) Between the Rigid Bodies they Connect
And the final joint is the helical (H), or screw joint that provides a simultaneous rotation and translation about a screw axis and can provide one degree of freedom. You can watch a short video HERE!
The difference between this joint and the cylindrical joint is that in the cylindrical joint, the rotation and translation are independent, thus providing us with two degrees of freedom (DOFs), but in the helical joint, this motion is simultaneous, so it only has one degree of freedom.
Grübler’s Formula to Find the Degrees of Freedom (DOfs) of Any Mechanism Including the Robots
Grübler’s Formula is a general formula that can be used to find the degrees of freedom of any mechanism and not just the robots.
Grübler’s formula says that the number of degrees of freedom is equal to the sum of the freedoms of the bodies minus the number of independent constraints put on the motion of those bodies:
If we take N as the number of bodies or links (note that we traditionally also take ground as one link):
and if we take J as the number of joints:
and if m is the number of degrees of freedom of a single body, that is six for spatial bodies and three for planar bodies:
Then we can write the degrees of freedom are equal to rigid body freedoms minus joint constraints. We deduct 1 from N because we want to exclude the ground:
We know that the degree of freedom of movement of one link w.r.t another can be found by deducting the number of constraints that the joint puts on the movement from the DOFs of a rigid body:
Rewriting the formula in terms of the DOFs of the joints we can get this formula:
This is called Grübler’s formula that can be used to find the degrees of freedom of any mechanism. Remember that all constraints are independent!
Now let’s see some examples.
Grübler’s Formula to Find the Degrees of Freedom (DOFs) of Planar Mechanisms
Two-Degree-of-Freedom (2-dof) Planar Robot Arm
We have seen that our planar two-link robot arm has two degrees of freedom (DOFs). Now let’s see if we can get the same answer with Grübler’s formula:
Four-Bar Linkage
Now let’s step it up a notch and find the degrees of freedom of a four-bar linkage. It has four links because remember we take the ground as one of our links too:
We could expect this result because the four-bar linkage is a 3R open-chain robot that the two ends are pinned, so three DOFs of the serial chain minus two constraints gives us one degree of freedom (DOf).
Keep in mind that for Grübler’s formula to work, the constraints must be independent.
The next examples are for spatial robots.
Grübler’s Formula to Find the Degrees of Freedom (DOFs) of Spatial Mechanisms
Stewart Platform
The first mechanism is a Stewart mechanism, which is a parallel mechanism with six legs. Each leg has two spherical joints and one prismatic joint. We can also replace the bottom spherical joints with universal joints with two degrees of freedom (DOFs). Because it is a parallel robot, each leg supports a fraction of the weight of the payload.
Now let’s find the degrees of the robot using Grübler’s formula:
Of these twelve degrees of freedom, only six degrees of freedom are shown in the top platform since the other six are torsional rotations about the leg axis and do not affect the mobile platform’s motion. Because the top platform can move with the full six degrees of freedom (DOFs) of a rigid body in space, the Stewart platform is usually used to simulate airplanes.
Delta Robot
Now let’s find the degrees of freedom (dofs) of a Delta robot.
Delta robot is a parallel robot that can maintain its end-effector orientation, unlike the Stewart platform that can change the orientation of its end-effector. It has three legs, and each leg has three Revolute joints, four spherical joints, and five links:
Of these fifteen degrees of freedom, twelve are related to torsion of the twelve links because of being connected to the spherical joints. These degrees of freedom are called internal degrees of freedom (DOFs). Only three are visible at the end-effector on the moving platform. Delta robot acts as an x-y-z Cartesian positioning device.
An Advanced Example
Consider a robot arm with seven degrees of freedom (DOFs) that mimics the seven degrees of freedom (DOFs) of the human arm (Three rotational degrees of freedom (DOFs) for the shoulder, one rotational degree of freedom (DOF) for the elbow, and three rotational degrees of freedom (DOFs) for the wrist):
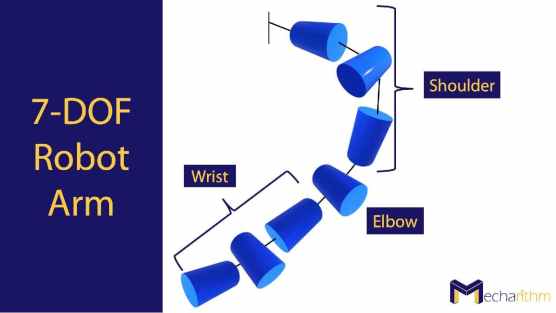
And assume that this robot should carry a tray with drinks on it. The drinks should not be spilled from the tray.

How many DOFs does the robot arm have while satisfying this constraint?
The answer to this problem is in the video below! Enjoy!
References:
Textbooks:
- Modern Robotics: Mechanics, Planning, and Control by Frank Park and Kevin Lynch
- A Mathematical Introduction to Robotic Manipulation by Murray, Lee, and Sastry
Videos:
