Fracture-Directed Steerable Needles
Our paper entitled “Fracture-Directed Steerable Needles” is published in the Journal of Medical Robotics Research.
The authors of this manuscript are Fan Yang, Mahdieh Babaiasl, and John Swensen.
Abstract of the “Fracture-Directed Steerable Needles”
Steerable needles hold the promise of improving the accuracy of both therapies and biopsies as they are able to steer to a target location around obstructions, correct for disturbances, and account for the movement of internal organs.
However, their ability to make late-insertion corrections has always been limited by the lower bound on the attainable radius of curvature.
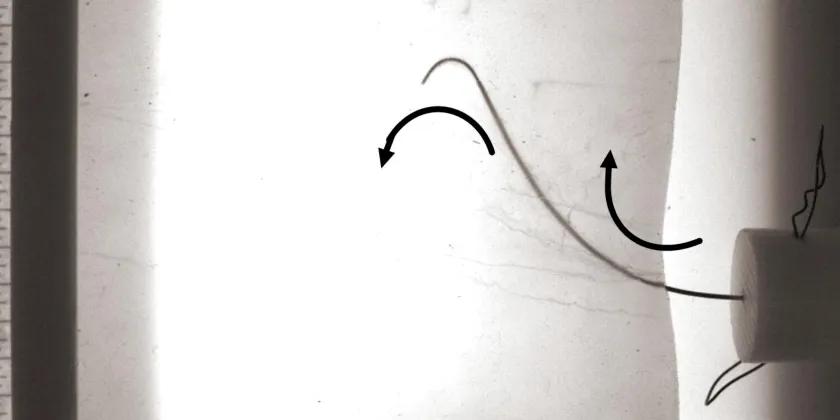
This project involves a new class of steerable needle insertion where the objective is to first control the direction of tissue fracture with an inner stylet and later follow with the hollow needle.

This method is shown to be able to achieve a radius of curvature as low as 6.9 mm across a range of tissue stiffnesses and the radius of curvature is controllable from the lower bound up to a near-infinite radius of curvature based on the stylet/needle step size.
The approach of “fracture-directed” steerable needles indicates the promise of the technique for providing a tissue-agnostic method of achieving high steerability that can account for variability in tissues during a typical procedure and achieve radii of curvature unattainable through current bevel-tipped techniques.
A variety of inner stylet geometries are investigated using tissue phantoms with multiple stiffnesses and discrete-step kinematic models of motion are derived heuristically from the experiments.
The key finding presented is that it is the geometry of the stylet and the tuning of the bending stiffnesses of both the stylet and the tube, relative to the stiffness of the tissue, that allow for such a small radius of curvature even in very soft tissues.
- Read a full pre-publication version of the paper HERE!
Materials and Codes Related to the Paper:
- You can find the Hardware including 3D printed parts, motors, etc. HERE!
- Codes written in C and Python for Needle Insertion Controller can be found HERE!
You can also find the MATLAB code for the kinematic model of the steerable needle based on Lie Groups and Lie Algebra HERE! The output of the code is as follows:

An overlay of the reality (experiments) with the simulation is depicted in the following photo:

Watch a short video of the Stylet and Tube Fracture-directed Steerable Needles Below:
How to Find the Equation of the Curve in a log-log Figure
Have you ever encountered a figure in a paper that the data are visualized in a log-log format and you wanted to extract the equation of the curve?
For the above paper, we had to do the same thing so we thought it may be useful for you too.
Suppose that we have a log-log plot like the following:

From the figure, we can write:
So, the equation can be written as:
To find c:
So, the equation of the log-log plot is:
